マーケティングリサーチの学び場『Lactivator』代表。自動車会社でマーケティングリサーチに従事後、誰でも気軽にマーケティングを学べる場として2012年に本サイトを開設。また故郷:群馬県の活性化の為、2013年より上毛かるたの日本一決定戦『KING OF JMK』を主宰。著書『上毛かるたはカタル』も発売中。
●無料メールで学ぶマーケティング講座配信中⇒こちら
こんにちは。マーケティングリサーチャーの渡邉俊です。
今日は、WEBビジネスでおなじみのA/Bテストについて徹底解説したいと思います。
Webサイトを使ってビジネスを行っている方であれば言わずもがなですが、それぞれのサイトには何かしらの目的があります。閲覧した人に自社商品を知ってもらう、または自社にコンタクトをしてもらう、商品を購入してもらう・・・などです。
その目的を達成する為には試行錯誤してサイトを改善していく必要があり、そこで重要になってくるのがA/Bテストです。
A/Bテストとは
A/Bテストとは『パターンA』 と『パターンB』のWEBページを作り、どちらのほうが訪問者の反応が良いのかを比較をするテストを指します。もちろん2パターンに限定している訳ではなくCやDがある時もありますが、パターンの数に関係なくA/Bテストと呼ばれています。
WEBサイトの目的とコンバージョン
そもそも個人の趣味でサイトを運営しているのならば別に気にしなくてよいのですが、ビジネスとしてサイトを持っているのであれば、きちんと『目的』をもって中身を設計しなければいけません。
例えばECサイトであれば何か特定の商品を販売している訳ですから、そのサイトに来て商品を見たお客さんが購入してくれるという流れにしたいですよね。
その際、訪問者100人あたり何人が購入してくれたかという割合をコンバージョンといいます。
ECサイトを運営している人は、このコンバージョンをできるだけ高くしたい訳です。
ちなみにコンバージョンはそのサイトの目的によって定義が異なります。
サイトの内の特定のページに誘導するのが目的であればそのページを閲覧した人の割合をコンバージョンと言いますし、メルマガに登録して欲しいのであればサイト訪問者のうちの登録者数の割合をコンバージョンと言ったりします。
WEB改善こそ『仮説』が命!
ではコンバージョンを高めるにはどうしたらよいか?という所に興味がいきますが、これに関して書くと本1~2冊できてしまうくらい奥が深いです。
WEBビジネスの経験を積めばある程度の原理原則みたいなものは分かるようになるのですが、基本的には、
- ここの文章はこう変えた方が商品の魅力をより分かりやすく伝えられるのではないか?
- ここ挿入したイラストは別のイラストにした方が閲覧者の気を惹けるではないか?
- そもそも文章のフォントを別のものに変えた方がこのサイトのイメージに合っているのではないか?
という細かい『仮説』を基にサイトをつくり、実際のお客さんの反応(コンバージョン)を見るのです。うまくいかなければまた別の『仮説』を試しコンバージョンが増えるかどうかを検証します。
このようにして、『仮説』があっているかどうかを1つ1つ、何度も何度も検証していってコンバージョンを高めていきます。
その際にやらねばならないのが「A/Bテスト」です。
※ちなみに仮説の設定はA/Bテストに限らずマーケティングでは重要なステップです。以下の無料メール講座でも詳しく説明していますので、この機会に是非読んでみて下さい。
A/Bテストを実行する
例えば、あるECサイトでパターンAとパターンBのページがランダムに開くように設定し、それぞれの訪問者数と商品購入者数をカウントしたところ、以下のような結果になりました。
パターンA 10,000人の訪問があり、そのうち100人が購入
パターンB 8,000人の訪問があり、そのうち120人が購入
この場合、パターンAのコンバージョン(購入率)は1.0%、パターンBは1.5%になります。
従いまして、パターンBをWEBサイトに採用すれば、0.5%高い成約率が見込めるんじゃないかな?となる訳です。
たかだか0.5%と思うかもしれませんが、月に50,000人の訪問があれば購入数に250件の差があります。これの商品単価が1万円だとしたら、パターンAをパターンBにしただけで月250万円の売上の差となるのですからバカにできませんよね。
しかし、ここで疑問が湧いてくるのが、上記の結果を本当に信用するかどうかです。
パターンAよりパターンBで購入率が0.5%高いというのは偶然の結果だったのかもしれません。
そういう疑り深い人って必ずいますよね(笑) でももちろんこの指摘は良い指摘だと思います。
その為、そういう人に対して回答するのに必要なのが統計学でいう『仮説検定』になります。
統計の知識を使うので難しい!と思う方もいらっしゃるかもしれませんが、これはとても重要なので是非覚えましょう。
【計算手順詳細】A/Bテストの仮説検定
上記の差の要因はパターンAよりBの方がお客様の購入意欲をそそるから起こったのか、それとも単なる偶然なのか(本当はパターンAもBも差はないのか)を判定する為に行うのが『仮説検定』です。
統計学の知識を使うのでちょっと難しいかもしれませんが、実はエクセル関数を使えば簡単にできてしまいます。
ただそれだと味気ないですし、計算の中身を知っておくのは必要なことなので、ここでは『どんな統計の計算を行って仮説検定しているのか?』を詳しくお話します。
※統計とか数学とか苦手という方の為に、なるべく簡単な言葉を使って説明するよう努力して書きました(笑) 是非歯を食いしばって読んでいただけると幸いです!
独立性のχ(カイ)二乗検定
WEBのA/Bテストの仮説検定でよく使われるのが『独立性のχ(カイ)二乗検定』と呼ばれるものです。
χなんてギリシャ文字が出てきた時点で数学っぽくてイヤ!と感じてしまうかもしれませんが、要するにここで行いたいのは、
●閲覧したWEBページ(パターンAとパターンB)
●商品の購入/非購入
この2つの軸が独立しているか否か?を計算で求めるということです。
『2つが互いに独立している』という事になれば、閲覧したWEBページと商品の購入/非購入は独立している(関連性がない)という事になります。つまりパターンAにしようがBにしようが購入/非購入に差はないという事です。
逆に『独立していない』という事になれば閲覧したWEBページと商品の購入/非購入は関連性があるという事になる(=パターンBの方がより多くの人の購入を見込める)訳です。
手順①:”パターンAとBの購入率は同等”と仮説を立てる
もちろんここでは、『閲覧したWEBページと商品の購入/非購入は関連性がある(=パターンBの方がお客様の購入率に効果がある)』と言えるのが理想です。
ただその為には、初めに『パターンAとBにおける商品購入率に差はない(互いに独立している)』と、今回主張したい事とは逆の仮説を立てます。(このように主張したい事の逆の仮説を統計学では『帰無仮説』と言います)
要するに、今回のA/Bテストの結果ではパターンBの購入率の方が高かった訳ですが、『これは単なる偶然だったのだ』という仮説をまず置くのです。
そして、この帰無仮説(パターンAとBには差が無い)の内容が発生する確率を統計学的に計算します。
この確率のことを統計学で『p値』と言うのですが、
- p値が小さい
⇒『帰無仮説のような事は起こりにくいのでパターンBの方が購入率に効果がある』 - p値が大きい
⇒『今回の結果はたまたまであり、パターンAとBで差があるとは言えない』
という事になる訳です。
通常、p値が大きいか小さいかは5%が基準になります。(もちろん5%でなければいけない訳じゃないのですが)
5%以下にならば今回のテスト結果は偶然に起きたものではないと判断し、つまりパターンAとBにはきちんと違いがあって、パターンBの方が購入率に効果があると言えます。
※p値については以下でも詳しく説明しています。
手順②:結果をクロス集計してまとめる
次に先程のA/Bテストの結果をクロス集計してまとめてみます。ちょっと固い言い回しになってしまいますが、これを観測値と呼びます。
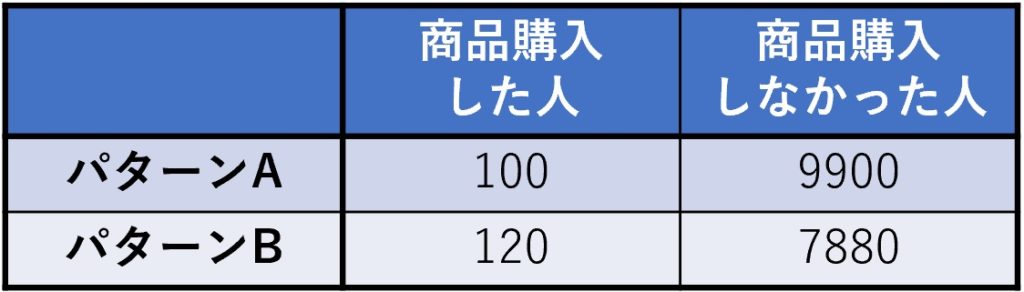
手順③:期待値を計算する
次に、このA/Bテストの期待値を計算します。
この期待値というのは、WEBサイトのパターンと商品の購入/非購入が独立しているとしたら、購入者、非購入者は何人になるはずか?という数字です。
パターンAとBを合わせて購入した人はは220人。逆に購入しなかったのは17780人なので、これをA、Bの訪問者数の比率で割ればよいことになります。
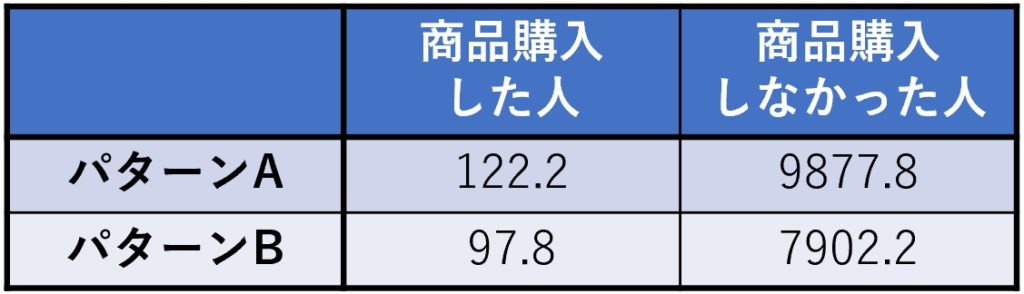
要するにパターンAであろうがBであろうが、購入/非購入に差がない(互いに独立している)のであれば上記のような結果になるはずです。
手順④:χ2検定量の算出
さて、ここからがちょっと難しくなるのですが、次に各セルの観測値が期待値からどのくらい離れているかを数値化します。
しかし、ただ観測値と期待値を引き算しただけでは数値処理上で問題があるので、ここでは
(観測値-期待値)2 / 期待値
という計算を各セルで行います。例えば左上のセルであれば、以下のような計算です。
(100 – 122.2)2 / 122.2 = 4.03
各セルで計算した結果は以下です。
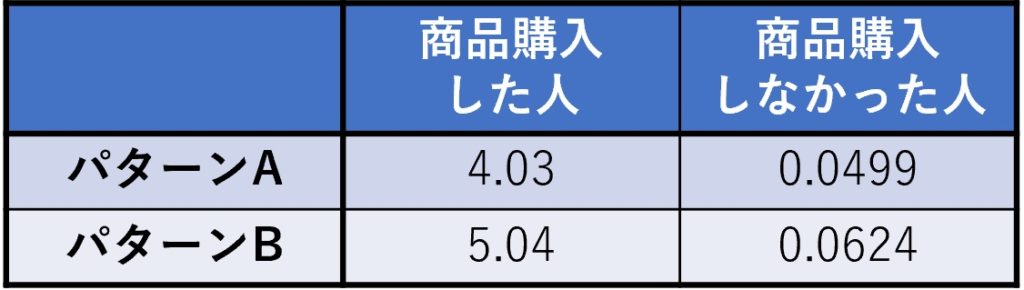
そして、これら全部を足し合わせた値をχ2検定量と呼びます。この場合は、
4.03 + 5.04 + 0.0499 + 0.0624 = 9.18
となり、9.18がこの場合のχ2検定量です。
このχ2検定量が大きければ大きいほど期待値の状態(2つの軸は完全に独立している状態)から離れているという事がお判りいただけますでしょうか?
もし完全に2つが独立しているのであれば、パターンA、Bそれぞれの購入/非購入は先程の期待値の表の通りになりますので、χ2検定量は0になるはずです。
しかし2つに関係性があるほどそれぞれのセルの値は期待値から外れていく事になるので、χ2検定量は大きくなっていく訳です。
手順⑤:検定結果を出す
そして当初の目的である『閲覧したWEBページ(パターンAとB)』と『商品の購入/非購入』は互いに独立しているのか否かの検定ですが、これは上で求めたχ2検定量の値を使います。
以下の曲線はχ2分布と呼ばれるもので、横軸はχ2検定量、縦軸はのχ2の頻度を示しています。
χ2の頻度というのは同じテストを何度も行った時、どのくらいの頻度で各χ2検定量がアウトプットされるかを示しています。
今回は『閲覧したWEBページ(パターンAとB)』と『商品の購入/非購入』が互いに独立している(何の関係もない)という帰無仮説を設定しましたが、その仮説が正しいのであればχ2検定量は0になる事が多くなるはずです。
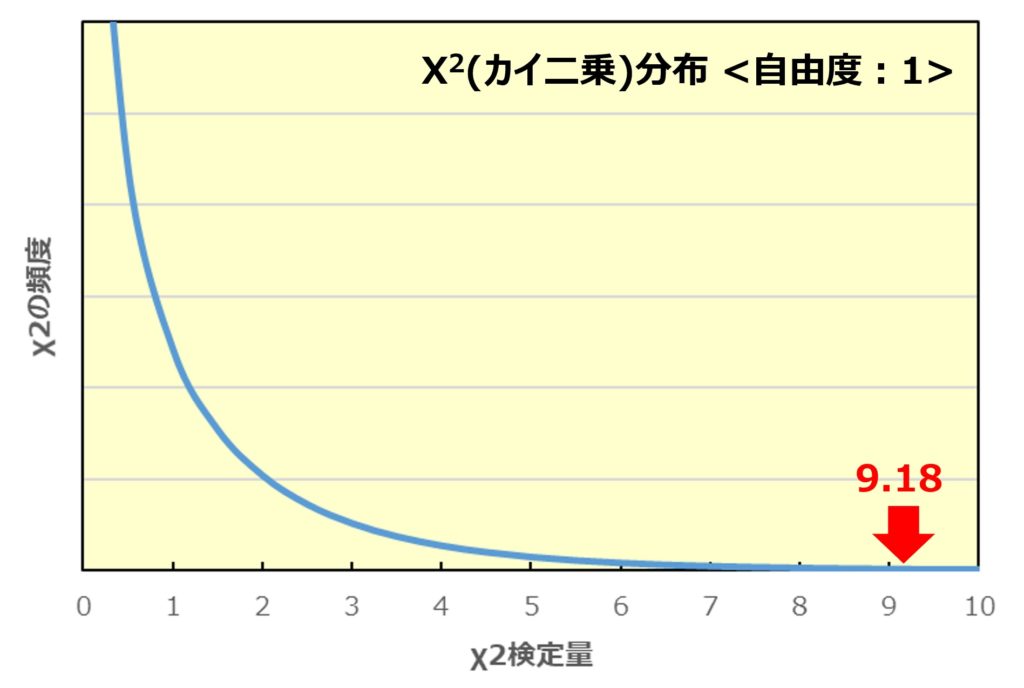
しかし当然『ばらつき』というものが存在するので毎回0にはならず、時には1になったり、2になったり、まれに3になったりします。ただ2つが完全に独立しているならばχ2検定量が大きくなるほどその頻度は小さくなっていくという事をこのグラフは示している訳です。
では今回算出されたχ2検定量は9.18でしたが、これはいったいどの位の頻度で起こるでしょうか?
上記のグラフの通りほとんど起こり得ません。
『閲覧したWEBページ(パターンAとB)』と『商品の購入/非購入』が互いに独立している(何の関係もない)のであれば、χ2検定量=9.18なんて値は滅多に起こらないということになります。
最初の方で説明した通り、マーケティング統計では発生確率(p値)が5%以下であれば『帰無仮説の内容は滅多に起こらない』と判断するのですが、上のグラフで見るとχ2 検定量が3.84以上であれば、そのデータが発生する確率は5%以下です。
今回χ2 検定量は3.84よりも大きい為、最初の帰無仮説『閲覧したWEBページ(パターンAとB)と商品の購入/非購入は互いに独立している(何の関係もない)』は棄却され、WEBページ(パターンAとB)と商品の購入/非購入には関係性がある(=パターンBの方が購入率が高いと言ってよい)と言えます。
補足:χ2分布と自由度
ちなみに先ほどχ2分布のグラフを出しましたが、これは正しくは自由度1の時のχ2分布になります。
統計学上の概念なのでちょっと分かりにくいかもしれませんが、自由度とは観測データのうち自由に値を取れるデータ数のことを指します。
今回のA/Bテストの結果を再度以下に載せますが、パターンAの閲覧者数は10,000人、パターンBの閲覧者数は8,000人、商品を購入した人は合計で220人と決まっています。
従いまして、検定に使う以下の4つのセルの数字のうち、1つのセルが決まってしまえば他のセルに入る数字は全部決まってしまいます。
言い換えれば、自由に値を取れるデータ数は1つしかないということです。

自由度はどんなA/Bテストを行ったのかによって異なってきます。
ただ上記のような2 x 2のクロス集計表における自由度は1と考えてよいです。基本的に自由度は(行数-1) × (列数-1)で計算できます。
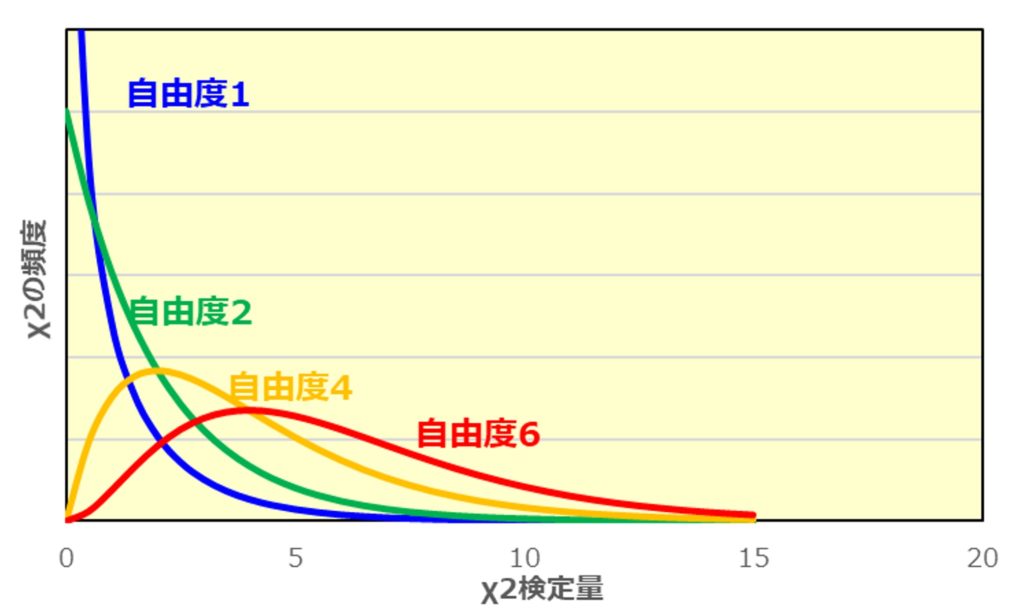
ちなみに自由度が異なるとχ2分布は以下のようになります。
なぜこのようになるかを説明するとなるとかなり長くなってしまいますので、それはまた今度・・・
エクセルで独立性のχ(カイ)二乗検定を行う
なるべく多くの方に分かっていただけるよう、χ(カイ)二乗検定の計算方法を書いたつもりです。
ただ世の中は便利なもので、上記の計算過程を理解していなくてもエクセルのCHISQ.TEST関数を使えば簡単にχ(カイ)二乗検定ができてしまいます。
やり方は簡単で、実測値が入力されているセルと期待値が入力されているセルを作り、
=CHISQ.TEST(実測値範囲, 期待値範囲)
と数式を入力すると以下のようにp値が算出されます。
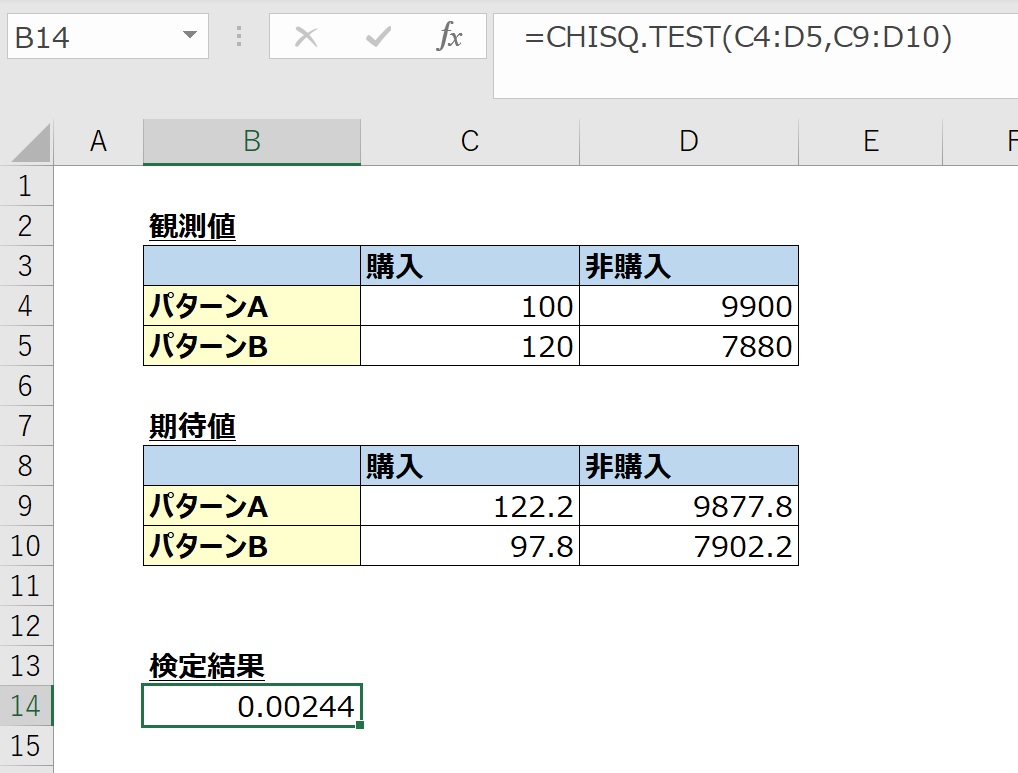
この場合、p値は0.00244とアウトプットされました。
先ほど申し上げた通り、マーケティング統計の場合p値は0.05以下(5%以下)であれば帰無仮説は棄却してよいので、エクセルの関数を用いても同様の結果になります。
まとめ
サイトを改善していく為にはA/Bテストが非常に重要です。
頻繁にやっている方もいらっしゃると思いますが、検定まで確実に行っている方は少ないと思いますし、行っていても検定の計算過程を認識している人は更に少ないと思います。
もちろん計算過程なんて知らなくても、上記のようにエクセル関数を使えば1分程度でできてしまうのですが、その計算の中身を知っておく事が重要だと思い、なるべく多くの方に理解してもらえるよう書いたつもりです。
是非、日々の仕事に役立てて下さい。
Lactivatorの動画講座を『Udemy』で配信中!
 Lactivatorが定期的に開催しているマーケティングリサーチの講座が、オンライン学習サービス『Udemy』に登場!
1つの単元を約10分前後の動画で解説しているので、通勤途中でもカフェでも、あなたの好きな時間に好きなだけリサーチを学ぶことができます。
最初の10分は無料で視聴いただけますので、是非ご覧ください!
Lactivatorが定期的に開催しているマーケティングリサーチの講座が、オンライン学習サービス『Udemy』に登場!
1つの単元を約10分前後の動画で解説しているので、通勤途中でもカフェでも、あなたの好きな時間に好きなだけリサーチを学ぶことができます。
最初の10分は無料で視聴いただけますので、是非ご覧ください!