こんにちは。
マーケティングリサーチャーの渡邉俊です。

今日のテーマは『相関』です。
統計学の本を開けば最初の方に書いてありますし、最近では高校でも習う？なんて話も聞くので知っている方も多いのではと思います。

『1とか-1に近ければ直線で、0だとバラバラっていうアレですね！』

という風に理解している人もいらっしゃるのではないでしょうか。

もちろんその通りなのですが、実は相関は間違って使うととんでもない目に合いますし、現にとんでもない目に合っている人を多く見ています。

そうならない為に、相関でマーケティングに関する何かしらの判断ををする時の注意点をまとめましたので是非読んで下さい。

相関とは

2つの関係が直線的であること

相関とは『一方が増えるともう一方も増える』、『一方が増えるともう一方は減る』という感じで2つの変数間に直線的な関係がある事を相関と言います。

例えば下の左側のグラフはある年の夏の期間中における『アイスコーヒーの販売個数』と『1日の平均気温』を散布図にしたものです。
平均気温が高ければ販売個数も増えるという関係がありそうですよね。
こういったものを相関関係にあると言う訳です。

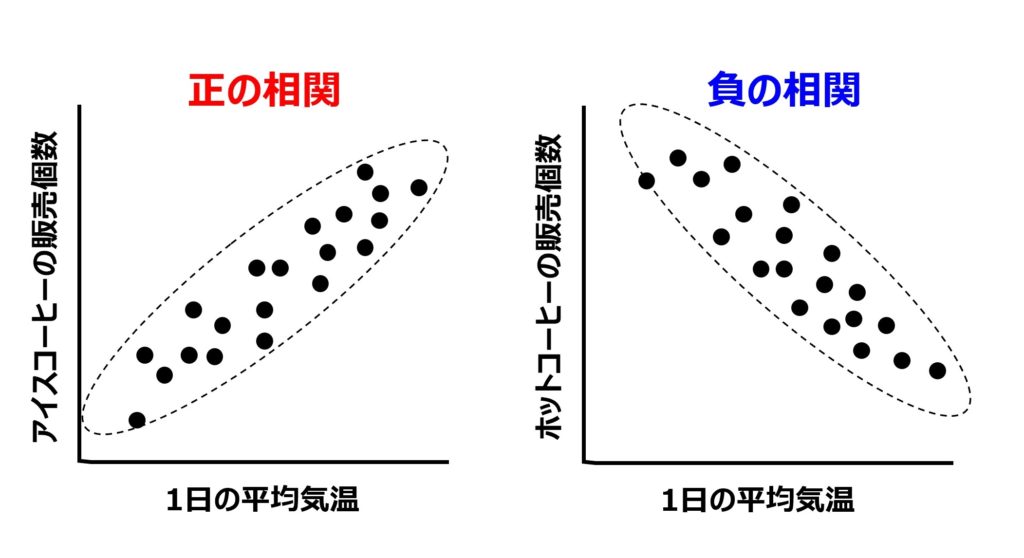
一方、右側のグラフはある年の夏の期間中における『ホットコーヒーの販売個数』と『1日の平均気温』を散布図にしたものですが、平均気温が高くなるほどホットコーヒーを買うお客さんは減る傾向にあります。これも相関関係です。

このように、

● 一方が増えるともう一方が増える関係⇒『正の相関』
(例：『アイスコーヒーの販売個数』と『1日の平均気温』)

●一方が増えるともう一方が減る関係⇒『負の相関』
(例：『ホットコーヒーの販売個数』と『1日の平均気温』)

と呼んでいます。

相関係数とは

相関を見る時に絶対に計算する必要があるのが『相関係数』です。
通常、相関係数というとカール・ピアソンという方が定式化した”ピアソンの積率相関係数”の事を指します。
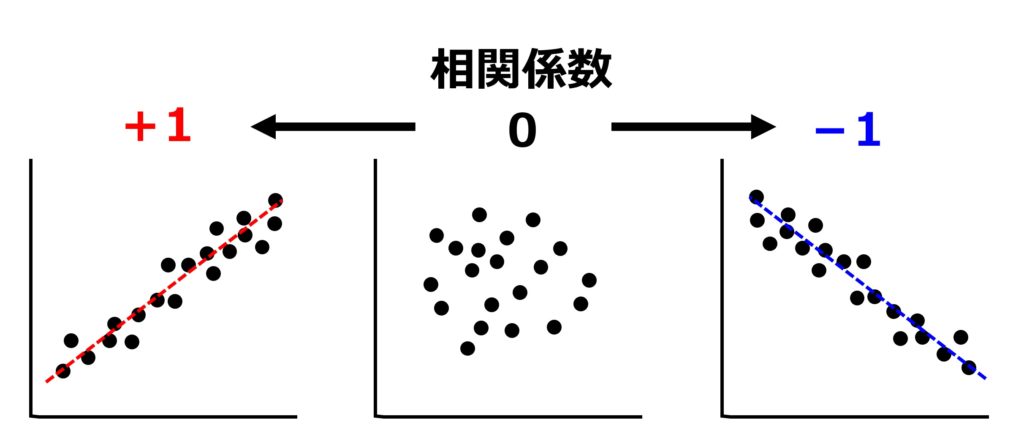
この係数は―１～＋１の値を取りますが、＋１に近くなるほど正の相関が強い、逆に－１に近くなるほど負の相関が強いということになります。
また０(ゼロ)に近い時は相関が無い（無相関）ということです。要は2つの変数には全く直線関係がないという事ですね。

エクセルで相関係数を算出する

ちょっと数学的な話になりますが、n組のxとyのデータ があった時、ピアソンの積率相関係数(r_xy)は下記のような式で求める事ができます。

 

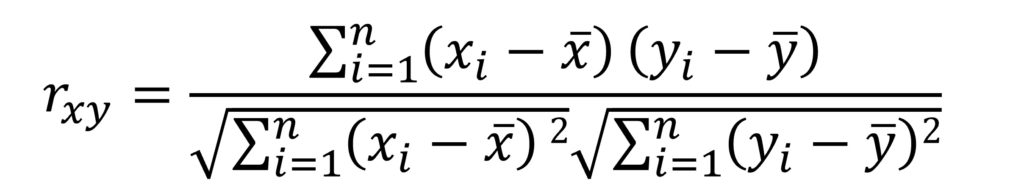
本当は、なぜこの式で相関係数が求められるのかを知ってほしいのですが、多分それを書くと数学嫌いの方はブログを読んでくれないのでやめておきます(笑)
知りたい方は他のWebサイトや多くの統計学の本で解説されているのでそちらをご参考にして下さい。

しかし、今この式に則って手計算で相関係数を求める人は皆無と言っていいほどいません。
手計算だと算出まで何時間もかかりますが、エクセルなどの表計算ソフトを使えば数秒で求められるからです。

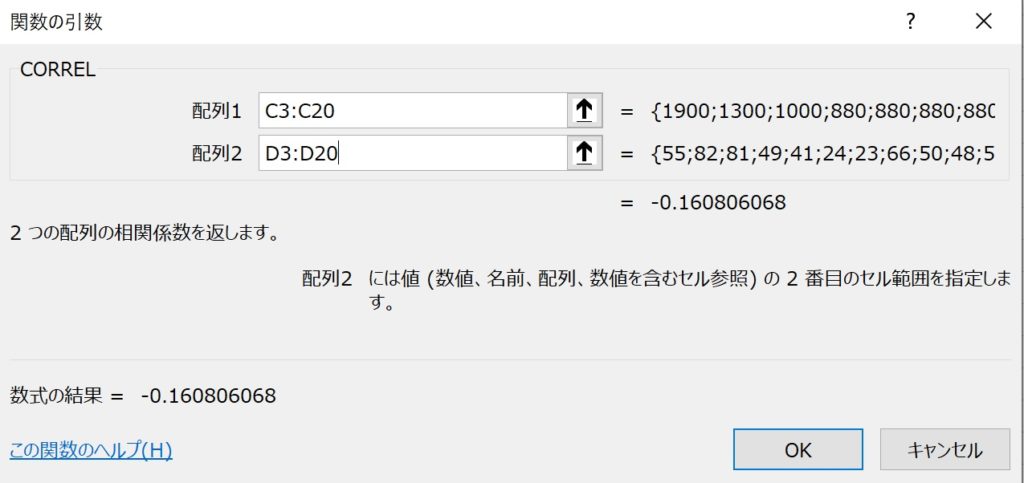
エクセルだと”CORREL”という関数を使えば一発ですね。
配列1と配列2にそれぞれ相関を調べたいデータを入れれば、すぐに相関係数が表示されます。

 

相関でよくある誤解

ここまでは既に知っているという方も多いと思いますが、ここからが本題です。
近年はコンピュータを使えば相関係数の計算なんぞ超簡単にできるようになってしまったので、結構軽く思っている人が多いのです。

ですが、冒頭でも申し上げた通り、軽く見るととんでもない目に合います。
マーケティングであれば、相関係数を間違って解釈する事によって間違った方向にビジネスを動かしてしまう可能性があるという事です。

注意すべき点を1つずつ紹介します。

相関係数が大きいからといって必ず線形関係とは限らない

まず相関を見る時にはただエクセルで係数を求めるのではなく、必ず散布図を描いてみてデータの分布をチェックして下さい。
例えば以下のような状態は、相関係数は0.8とかなり高いですが、2つの外れ値(何かしらの原因によって異常とみなされる値)に引っ張られて計算上そうなっているだけです。
実際にこの2つの値を外して計算すると相関係数は0.04となり、本当は全く相関はありません。

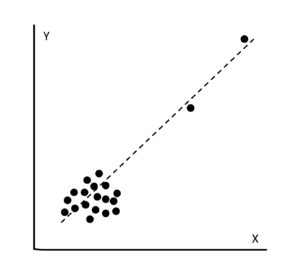
また以下は、相関係数を求めると0.65とそこそこ高いのですが、散布図を描いてみると線形ではない別の関係性がありそうですよね。

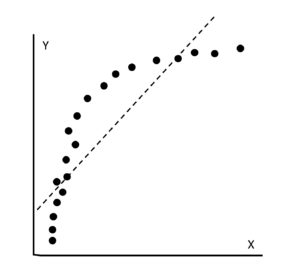
このように単純に相関係数が高いからと言って線形性の関係があると決めつけるのではなく、散布図を描くという作業を面倒くさがらずにきちんとやってみて下さい。

相関係数が小さいからといって全く関係性がないとは言えない

逆に相関係数が小さいからといって何の関係性もないと決めつけてもいけません。
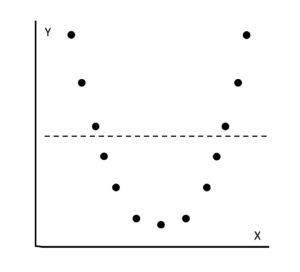
以下は相関係数0の散布図なのですが、明らかに別の関係がありそうですよね。

これも相関係数を計算するだけでなく、散布図を描くことによって気づくことができます。

相関係数で『因果関係』は説明できない

混同している方が非常に多いのが『相関関係』と『因果関係』です。

基本的に相関が強いという事はその2つの変数の間に線形関係があることを示していますが、因果関係までを説明できるものではありません。
言い換えればAとBの間に強い相関関係がある時、

●Aが増えればBも増える(または減る)
●Bが増えればAも増える(または減る)
●上記2つの両方が成り立つ

の3パターンが考えられますが、どれが当てはまるかは相関係数は何も教えてくれないのです。

例えば一番最初に示した『アイスコーヒーの販売個数』と『1日の平均気温』の相関関係であれば、

『1日の平均気温』が高いほど『アイスコーヒーの販売個数』も増える。

という因果関係が成り立つことは誰でもわかると思います。
間違っても『アイスコーヒーの販売個数』が増えると『1日の平均気温』も高くなるとは考えないですよね。
もしそうだとすれば、国民全員がアイスコーヒーを飲んだらその日の平均気温はどえらい数字になってしまいます(笑)
なので、これは経験的に因果関係の矢印の向きを推定している訳です。

しかし、例えば、『数学の期末試験の点数』と『1日の中でゲームに費やす時間』が負の相関関係にあるとしたら、どのような因果関係があるか分かりますでしょうか？

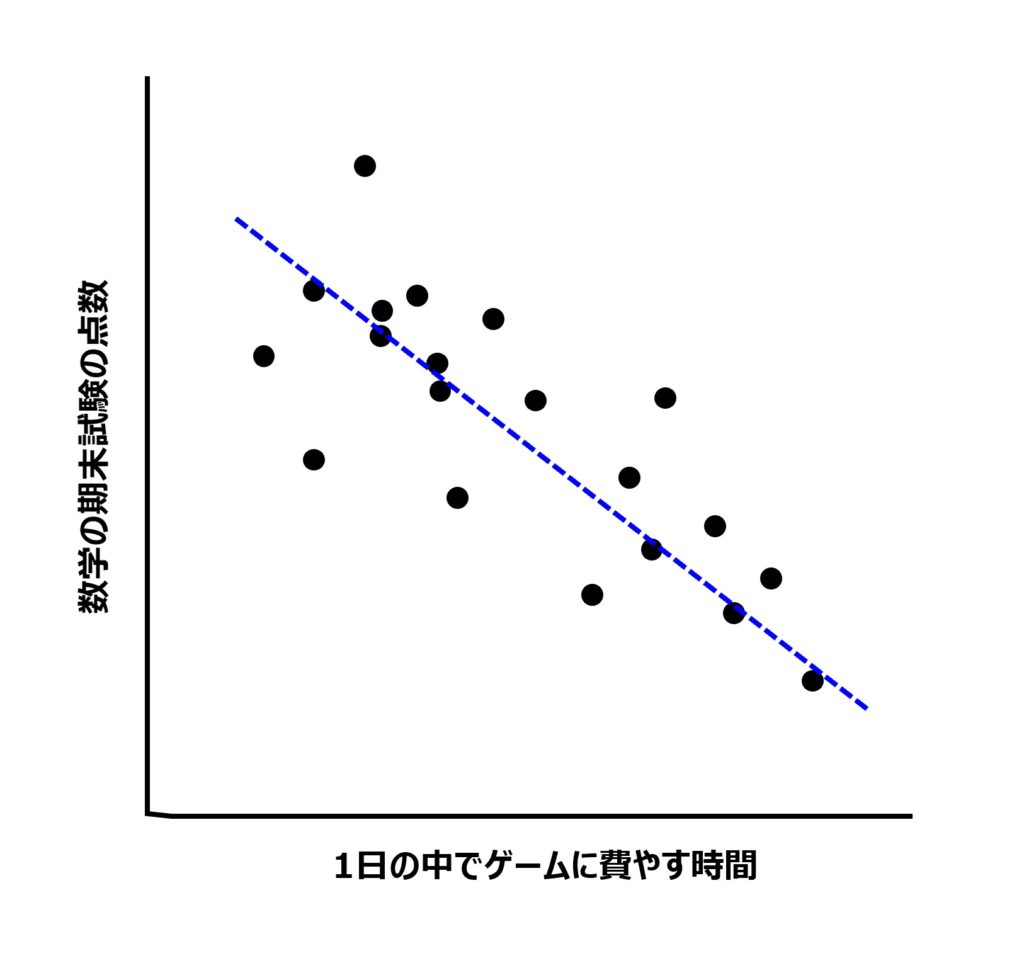
普通に考えるとゲームばかりやっているから数学の点数が低いんだ！と思ってしまいがちですが、もともと学習意欲の低い学生ほどゲームにはまってしまいがちであるとも考えられ、因果関係の矢印の向きはわかりません。

矢印の向きがどちらなのかは相関分析では掴みようがないのです。

疑似相関の可能性

また相関分析には、『相関係数は高いけど、実際に相関関係はない』という事もありえます。
例えば数十年前、あるアメリカのハウスメーカーさんでは『握力の強さと貯金額の多さは負の相関がある(握力が弱い人ほど貯金額が多い)』という噂が信じられていたそうです。

その為そのメーカーの営業マンは、モデルハウスを見学に来たお客さんとは初めに必ず握手をし、握力の強さを確認した上でセールストークをするかどうかを決めていたという話があります(笑)

さすがに握力の強さと貯金額の多さの相関を調べた事はありませんが、常識的に考えれば上記が本当とは思いませんよね。
当時の人が調べたのかどうかは定かではありませんが、考えられるのは『握力の強さ』と『貯金額の多さ』の疑似相関です。

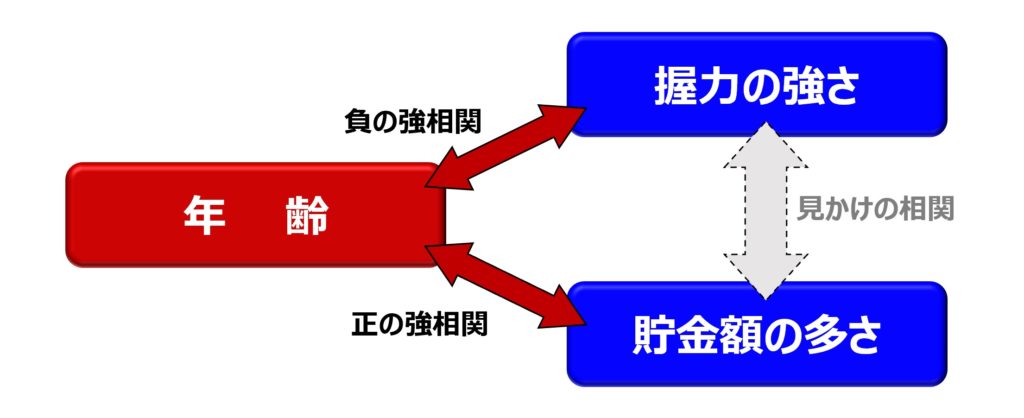
一般的に握力というのは年齢と共に弱くなっていきますが、逆に貯金額は年齢と共に多くなります。
『年齢』という第3のファクターを間に挟むことによって、全く関係のない2つの変数が相関のあるように見えてしまうのです。

このように2つの変数に相関関係がないのに、見えない要因（潜伏変数）によって高い相関係数を示すことを『疑似相関』と言います。

上記のハウスメーカーの話は笑い話ですが、実際にビジネスにおいてはこのような疑似相関を信じてしまうケースは多々あります。
疑似相関はどうかを見抜くには『偏相関係数』という数値を求める必要があるのですが、ちょっと難しい話になりますのでまた別のブログでお話することにします。

まとめ

いかがでしたでしょうか。
相関係数は統計学の中でも比較的広く知られているので、多くの方がビジネスに活用していると思いますが、軽く使うと痛い目に合います。
どっぷりと統計学の話をすると難しくなってしまうのですが、まずは

● 単に相関係数を求めるだけでなく、散布図を描いてみる。
● 相関係数は因果関係までは教えてくれないので、分析者が都度判断する。
●疑似相関になっていないかを分析前によく考える。
(第3のファクターが介在していないかを考える)

という事をまずは注意点として知っていただければと思います。

Lactivatorの動画講座を『Udemy』で配信中！

Lactivatorが定期的に開催しているマーケティングリサーチの講座が、オンライン学習サービス『Udemy』に登場！ 1つの単元を約10分前後の動画で解説しているので、通勤途中でもカフェでも、あなたの好きな時間に好きなだけリサーチを学ぶことができます。 最初の10分は無料で視聴いただけますので、是非ご覧ください！