マーケティングリサーチャーの渡邉俊です。

先日の科学論文誌『Nature』にある声明が800人超の署名入りで掲載されました。

それは、「統計的に有意差がない為2つのデータには差がない」という結論の導き方は統計的に誤りだというものです。

これは科学の世界のみでなく、マーケティングリサーチの世界でも同じように間違って解釈している方がかなり多いはずです。

 

『有意差』とは何か？

調査結果には『偶然』もあり得る

そもそも統計学を知らない方にとっては『有意差』という言葉自体初めて聞くかもしれませんが、アンケートなどの定量調査を分析する時には知っておく必要があります。

一言で言うと有意差とは『偶然とは考えにくい差』です。
アンケート調査では、複数のデータの差を見る時に有意差があるのか否かを検定します。

例えば、あるジュエリーブランドが出したテレビCMがブランドイメージ(高級感)にどの程度効果があったのかを調査によって検証する時。

この場合のやり方としては、

●テレビCMをグループA(200人)に強制視聴させ、このブランドに『高級感』のイメージを持っているか否かを聴取。

●他方のグループB(200人)には視聴させない状態でこのブランドに『高級感』のイメージを持っているか否かを聴取。

 

という形で効果検証します。その結果が以下のグラフです。

 

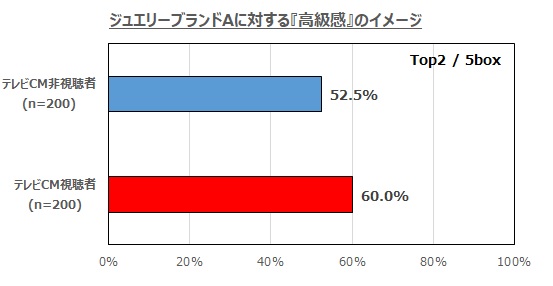
これを見ると、グループB(テレビCM非視聴者)で『高級感』イメージがあると答えた人は52.5%、一方グループA(テレビCM視聴者)では60%。
という事は、この時点ではテレビCMを視聴させたことにより『高級感』のイメージを7.5%向上させたと見る事ができる訳です。

 

有意差=偶然とは考えにくい差

但し、『このテレビCMはブランドイメージ向上に効果があるぞ！』と喜ぶのはちょっと早いのですね。
ここで出てくるのが『有意差』という概念です。

要するに、

『今回の調査では7.5%の差が出たけど、これって偶然じゃないの？』
『本当は効果ないけど、偶然こういう調査結果になっちゃったんじゃないの？』

という可能性もあります。

調査結果というのは「偶然そうなった」という事もあり得ます。
ですから、出てきた結果が偶然なのか否かをきちんと検定する必要があるのです。
それを『有意差検定』と言います。

 

有意差を検定する

有意差検定というのは統計学的な計算によって実施します。
ですが、今回細かい計算方法は割愛します。(後日、別のブログで書きます！)

本当は説明したいのですが、統計学の基礎的な事から書き始めなければならず膨大な文になってしまいますので(笑)

ただ計算の概要をお話しすると、検定の手順としては以下です。

まず、対象となるジュエリーブランドに対して、

●テレビCM視聴者が『高級感』イメージを抱く確率を『X』
●テレビCM非視聴者が『高級感』イメージを抱く確率を『Y』

とします。

そして、

①『X=Y』という仮説を置く。(テレビCMで高級感イメージは向上しない！という仮説を置く)

②もし上記仮説の状態であった場合、調査をするとXとYの間にどの程度誤差が生じる可能性があるかを計算によって求める。

その誤差と今回の調査結果を比べ、

③誤差範囲にある可能性が高い場合：
　⇒仮説は棄却されず、本当はX=Yであり今回の調査結果は誤差であった。(調査で出た差は偶然)

④誤差範囲にある可能性が低い場合：
　⇒仮説は棄却され、X=Yではなく実際に差がある。(調査で出た差は偶然ではない)

という風に処理をして、偶然なのか意味のある差なのかを検定するのです。

 

検定結果を決定する「p値」

その検定を行う時に算出するのが「p値」という数値です。
これも概念だけ申し上げると、p値というのは『仮説の元で、検定する統計量がその値(実際の調査結果)となる確率』の事を指します。

従いまして、p値が小さいほど『本当にX=Yなのであれば、今回の調査結果の様にはなりにくい』ということになり、仮説は偽として棄却します。
その棄却するp値をいくつにするかは分析者によるのですが、一般的には5％または1％以下に設定します。

上記のジュエリーブランドのデータの場合、p値は13%程度です。

これだと統計学的には確率が高いので『X=Y』という仮説は棄却されず、テレビCMがブランドイメージに効果があったとは言えないということになります。

 

【超注意事項】『有意差がない』時の解釈

『有意差がある』の反対は何？

さて、ここが問題です。
今回のジュエリーブランドの例では有意差検定を行った結果、『テレビCMがブランドイメージに効果があったとは言えない』と書きました。

この時ほとんどの分析者が、『有意差がある＝テレビCMに効果がある』のであれば

『有意差がない＝CMに効果がない』

と解釈してしまいます。これが大きな間違いです。

今回の『Nature』の声明でも、統計的な有意差がない場合でもそう結論付けてはいけないと言っています。

『有意差がある』の反対は『有意差があるとは言えない』

です。

 

帰無仮説と対立仮説

先程の検定手順で述べた通り、『X=Y』(テレビCM視聴者と非視聴者で『高級感』イメージに差はない)という仮説を作り、これを棄却できるかどうかで有意差を検定しました。

このような仮説を『帰無（きむ）仮説』といいます。
帰無仮説とはとりあえず立てた仮説（ほとんどの検定者が否定したい仮説）です。

そして、帰無仮説が間違っていると確信できる（棄却できる）時に選ぶものを『対立仮説』と言います。

多分読んでいてもややこしいと思うので何度も書きますが(笑)、
今回の場合だと、

• 帰無仮説：テレビCM視聴者と非視聴者で『高級感』イメージに差はない。(X=Y)
• 対立仮説：テレビCM視聴者と非視聴者で『高級感』イメージに差がある。 (X≠Y)

という事になります。

注意しないといけないのは、帰無仮説が棄却できなかった場合は対立仮説を採用する事はできませんが、帰無仮説が正しいとも言えないという事です。

「有意差があるとはいえない」というあいまいな表現になり、「有意差がない」という事ではないのです。

しかし、Natureの声明によると、科学の世界でも「有意差がない＝効果がない」と間違った推論をする論文がかなり多いそうです。
実際、調査した5つの論文誌(791文献)のうち51％に誤りがみられたと言っています。

※ちなみにマーケティング調査について陥りやすい誤解を以下の無料メール講座で解説しています。
この機会に是非購読してください。

 

まとめ：有意差とは何かをきちんと理解すること！

統計学を知らない方にとってはちょっと難しい話だったかもしれません。
ただ、これはマーケティングリサーチをやっていくと必ずどこかで勉強しないといけない事なんです。

しかし先ほども申し上げた通り、有意差というものについて誤解しているマーケッターは数多く存在します。
実際私自身も、上記の事は分かっているものの、つい間違った解釈をしてしまう事があります(笑)

是非、ここでビシッと頭の中に叩き込みましょう。

 

Lactivatorの動画講座を『Udemy』で配信中！

Lactivatorが定期的に開催しているマーケティングリサーチの講座が、オンライン学習サービス『Udemy』に登場！ 1つの単元を約10分前後の動画で解説しているので、通勤途中でもカフェでも、あなたの好きな時間に好きなだけリサーチを学ぶことができます。 最初の10分は無料で視聴いただけますので、是非ご覧ください！