こんにちは、マーケティングリサーチャーの渡邉俊です。

今日はリサーチには付きものである『異常値』の検出方法とその取扱いについてお話します。
アンケートなどの定量調査を分析する際、『あれ？なんでこんな数字が出てきたんだろう？』ということが往々にしてあります。
しかしそれを異常値として除去していいのかどうか判断に困ることも多々あります。

そんな時にどう対処すればよいかをまとめましたので是非読んで下さい。

『外れ値』と『異常値』の違い

まず、『異常値』と似た様な言葉で『外れ値』という言葉があります。
ほぼ同じように用いられることが多いような気もしますが、基本的に異常値と外れ値は意味が違います。

『外れ値』とは、リサーチで測定または回収した他のデータと比べて極端に大きな値かもしくは極端に小さな値のことを指します。
そして、その外れ値の中でも、回答者の入力ミスやデータを入力した人のミスなどで極端にかけ離れているものが『異常値』です。
従いまして、「外れ値=異常値」とは限りません。

例えばある団体に加入している人の体重のデータで『200kg』という数字があった場合、一般の人の体重からは大きくかけ離れている外れ値ではありますが、異常値かと言われると悩みますよね。

現にお相撲さんなどで200kgを超える人はある程度いる訳ですから、その人に会って確かめてみない限りは異常とは言い切れない訳です。

もちろん『異常値』なのであればデータ分析から除去する必要があります。
ただそれを異常値なのかどうかを判断する為には、きちんと確かめないといけません。

グラブスの検定

大体の場合、外れ値なのか否か、異常値なのか否かの判断は分析者の感覚で決めてしまいます。
『これは明らかに変な値だから分析から外そう！』というその時々の感覚です(笑)
しかしそれは言い換えれば『恣意的』にデータを除去したとも捉えられてしまうので、本来はよくありません。

一応、外れ値か否かを判断する為に『グラブスの検定』という方法がありますので一応紹介しておきます。

異常値か否かの検定

グラブスの検定とはスミルノフ・グラブスが考案したものであり、極端に大きいまたは小さい値が異常値か否かをを検定するものです。

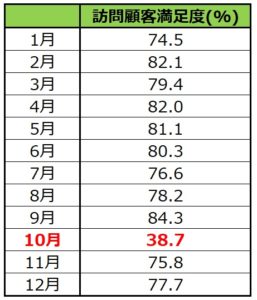
例えばあるお店で、来店客の中から毎月1000人にサービスの満足度を聴取したとします。
右の表はその際に『満足した』と回答した人の割合です。

ほとんどの月で80%前後の値となっているのに対して10月だけ38.7%と極端に低く、「これって調査方法か何かにミスがあった異常値なんじゃない？」と思いますよね。
ただ何の根拠もなくこの数値を除去してしまうと、自分に都合の悪いデータを隠したと言われかねません。
きちんと統計学的な根拠で大きく離れた値であり、「だからこの値を異常値として除外しました」と言いたい訳です。

そんな時にグラブスの検定を使います。

かけ離れた値の発生確率を算出する

グラブスの検定の考え方としては、

●平均値および正規分布からどれだけ離れた値なのか？
●その値はどのくらい確率で発生するものなのか？

を計算により算出します。

そして、『平均値および正規分布から大きく離れている』かつ『それが発生する確率は著しく低い』ということであれば異常値だと断定できる訳です。
その際、「発生する確率が5%未満」であれば異常値として扱う事が多いです。

グラブスの検定はエクセルなどの表計算ソフトがあれば実施可能です。
その為、ここではエクセルを使って行う方法を紹介します。

①仮説を立てる

まず検定なので帰無仮説を置きます。

帰無仮説：その値(38.7%)は異常値ではない。

『検定』を解説した時にも書きましたが、帰無仮説が棄却されるか否かを検定します。

②平均と分散を求める

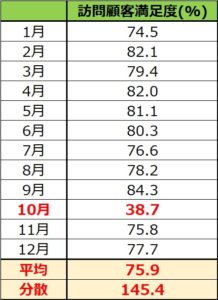次にデータの平均と分散を求めます。
今回の顧客満足度のデータは毎月1000人から聴取しているので、加重平均ではなく単純平均を採用します。

また『分散』という言葉について知らない方もいると思いますが、ここでは『データのばらつき度合』を数値化したものだと考えて下さい。

エクセルの場合、単純平均はAVERAGE関数、分散はVAR関数で簡単に計算できます。
それらの関数を使って右記のデータから計算すると、単純平均は75.9、分散は145.4となります。

③検定統計量を求める

ここまでできたら、次に『検定統計量』というものを求めます。
検定統計量(=t)とは、②で求めた平均値をX_ave、分散をσ、また異常値はどうかを知りたい値ををX_iを置くと、

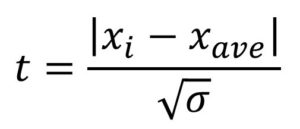
で求められる数値です。

分子の『｜　｜』は、異常値か否かを知りたい値と平均値の差の”絶対値”を指しています。
分母の分散がなぜ平方根になっているのか？はここでは説明を割愛しますが、要するにこの値は

●異常値か否かを知りたい値が平均から離れていればいるほど、tは大きくなる。
●分散が小さいほど(データ全体がバラついていないほど)、tは大きくなる。

データが全体がバラついていないのに検定の対象とする値が平均から離れていればtは大きくなりますので、この数値の大きさによって異常値か否かが判断できる訳です。

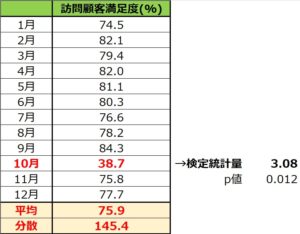
上記のデータをこの式に入れ込むと、

(75.9 – 38.7) / √145.4 = 3.08

この値が今回の検定統計量になります。

④p値を求める

最後に求めた検定統計量のp値を求めます。
聞きなれない言葉が連続して出てきているかもしれませんが、p値というのは『仮説の元で、検定する統計量がその値(実際の調査結果)となる確率』の事を示しています。

上記でも書いた通り、今回は帰無仮説として、

帰無仮説：その値(38.7%)は異常値ではない。

と置きました。そしてその検定統計量は3.08と算出された訳ですが、『じゃあこの3.08ってどのくらいの確率で起こるの？』というのがp値です。

これもエクセルでは、TDIST関数を使って求める事ができます。

TDIST(X, 自由度, 分布の指定) = TDIST (3.08, 10, 2) =0.012

自由度というのは別のブログで詳しく説明しますが、この場合は(データの個数－2)を選びます。
今回の場合、データは12個ありますので自由度は10になります。
また尾部は片側検定(=1)か、両側検定(=2)かを選ぶのですが、今回は両側検定になるので2を選びます。

そうするとこの場合のp値は0.012と算出されます。

これは『統計検定量が3.08になる確率は1.2%』ということを示しています。
上段でも書きましたが、通常は発生確率が5%未満(p値が0.05未満)であれば帰無仮説を棄却します。
統計検定量が3.08 (顧客満足度が38.7%)になる確率は1.2%と極めて低いので、今回は異常値とみなすという事が論理的に言える訳です。

以上がグラブスの検定を使った異常値の判定です。
統計学の知識がないとちょっと難しいかもしれませんが、こんなのがある事を是非覚えておいてください。

外れた値は何でも除去すればよい訳ではない

上記のグラブスの検定は、あくまで異常値か否かの判断に迷った際に使用します。
ただ、そんなことをしなくても明らかにこれは測定ミスか入力ミスだと判断できる場合もたくさんあります。
そんな時にはいちいち検定などしなくても取り除いて結構です。

例えば、体重測定を行った記録のなかに、685kgという記載があった時にはどう判断するでしょうか。
おそらく、データ入力する際のミスではないかと考えられますよね。例えば“68.5kg”の小数点が抜けてしまい“685kg”と入力しまったという場合です。

このようにある程度原因が分かるもの、または明らかに異常値だと言えるものはわざわざ検定なんてしなくても除外してしまって構いません。

ただ、”外れ値”は何でもかんでも除去するというのはよくないです。
例えば上記の10月の顧客満足度：38.7%は明らかに異常値なので除去しましたが、これが『異常値ではない』という検定結果が出た場合、『なぜこのような結果が出たのか？』をきちんと考察する必要が出てきます。

もしかしたら10月だけ、お客様の満足度を下げる何らかの要因があるかもしれず、それが今後も発生する可能性がある訳ですから。

繰り返しますが、『異常値』は除去しないと正しい分析ができません。
但し『異常値ではない外れ値』は、その原因を知ることで新たな発見につながる可能性があるのですから、そこをきちんと考えましょう。

Lactivatorの動画講座を『Udemy』で配信中！

Lactivatorが定期的に開催しているマーケティングリサーチの講座が、オンライン学習サービス『Udemy』に登場！ 1つの単元を約10分前後の動画で解説しているので、通勤途中でもカフェでも、あなたの好きな時間に好きなだけリサーチを学ぶことができます。 最初の10分は無料で視聴いただけますので、是非ご覧ください！