マーケティングリサーチの学び場『Lactivator』代表。自動車会社でマーケティングリサーチに従事後、誰でも気軽にマーケティングを学べる場として2012年に本サイトを開設。また故郷：群馬県の活性化の為、2013年より上毛かるたの日本一決定戦『KING OF JMK』を主宰。著書『上毛かるたはカタル』も発売中。
●無料メールで学ぶマーケティング講座配信中⇒こちら
●LINEでも最新ブログ、YouTube情報を配信中↓
こんにちは、マーケティングリサーチャーの渡邉俊です。
今回はアンケート調査を行うことで必ず発生する『誤差』について解説したいと思います。
アンケートには必ず『誤差』がある
『全数調査』と『サンプル調査』
例えば皆さんが『日本国民の中でプロ野球ファンは何%存在するか？』をアンケート調査で明らかにしたいとします。
さて、どんなアンケートを行えば一番正確に算出することができるでしょうか？
正解は『日本国民全員にアンケートに回答してもらう』です。”あなたはプロ野球ファンですか？”と全国民に質問して、『はい』と答えた人の人数を数えれば正確な数を把握することができますよね。これによって出てきた数字が真の値です。これを『全数調査』といいます。
ただご想像の通り、国民全員にアンケートを回答してもらうというのは超大変な作業になりますし、数十億～数百億円単位の超莫大な調査コストも発生します。はっきり言って国家レベルで動かない限り不可能なことなのです。
しかし、だからといってこの調査はできないのかというとそんなことはありません。
一番良い方法は、日本国民の中から一部の人たちをランダムに選んでこのアンケートに回答してもらい、『はい』と答えた人の割合を算出すれば、日本全体でプロ野球ファンが何%いるのかを『推定』することができます。
あくまで推定なので正確な値ではありませんが、近い値を知ることができる訳です。
実はあなたも普段の生活の中でこれと同じようなことをやっています。
例えば自宅で味噌汁を作っている時。あなたは鍋に火をかけて出汁を取り、豆腐や大根などの具材を入れ、そして最後に味噌を溶きますよね。これで味噌汁は完成なのですが、ただこの味噌の加減がちょうどいいのかどうかを念のため確認しなければいけません。
皆さんだったらどのようにして確認するでしょうか？一番正確に確認するのであれば、作った味噌汁を全部飲んでみることです。
そうすれば味噌がちょっと薄かったとしても発見することができます。でも味の確認の為だけに飲み干してしまったら何のために作ったのか分からなくなってしまいますよね。おそらくはお玉などで味噌汁をちょっとすくい、ズズッと飲んで確認するのではないでしょうか？
これがまさにアンケート調査と同じ行為になります。
要するにアンケートも味噌汁の確認も、ある集団全体の傾向や特性を知る為にその集団の一部を抽出して調査していることに他なりません。こうすることで、100%正確ではありませんがおおよその傾向や特性を知ることができる訳です。
このように、ある程度の誤差は考慮の上で集団から一部を抜き取り調査することを『サンプル調査』といいます。
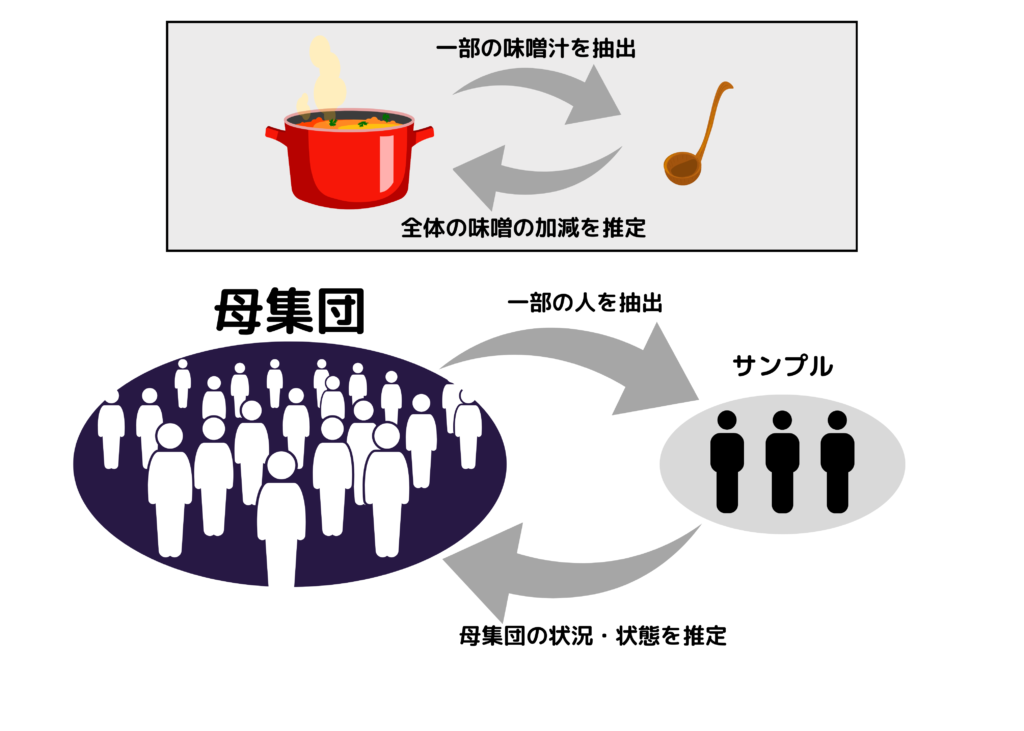
また調査によって状況・状態を知りたい集団全体の事を『母集団』といいます。
先ほどのように『国民の中にプロ野球ファンは何%存在するか？』を1000人にアンケートを配布して調べたい場合、知りたいのは”1000人の中でのファンの割合”ではなく”国民全体の中でのファンの割合”ですよね。なのでこの場合、日本国民全体という母集団の状況を推定する為にサンプルを1000人ランダムに選び、調査をする訳です。
これはとても重要なことなので、もう一度言います。
アンケート調査というのはサンプルを抜き出して母集団の推定を行う為の調査だということを是非頭に入れて下さい。
アンケートには”誤差”が付き物
ただここで気を付けなければならないのは、先ほどちょっと触れましたがアンケートには必ず『誤差』があるという点です。
例えば1000人に回答いただいた調査結果でプロ野球ファンの割合は40%と算出されたのならば、母集団である日本国民全体でも40%だ・・・とは言い切れません。サンプル調査の結果と母集団の実態には必ずズレがあるからです。これを誤差と呼んでいます。
これについては後で詳しくお話しますが、基本的にはサンプルサイズが母集団のサイズに近づいていくほど小さくなっていきます。
2024年1月現在、母集団となる日本国民は1億2400万人います。従いまして”あなたはプロ野球ファンですか？”に対する回答がたった10名だけだとかなり大きな誤差なのでデータとして使えませんが、100名、1,000名、10,000名と増えるにつれて誤差も小さくなります。
そしてもし回答を国民全員から獲得できたとしたら誤差は完全にゼロになるのです。
その為、”アンケートで集める回答の数はどのくらいにすればよいのか？”という質問を多くの方から受けます。
カンの良い方なら今の話を聞いてピンと来るのではないかと思いますが、その回答は『どのくらいの誤差を良しとするか？』に依るのです。
※詳細はこちらのブログでも紹介していますのでご覧ください！
ランダムサンプリングの原則
またもう1つ、アンケート調査を正しく行う上で知っておいて欲しいのは、回答する人は母集団の中から『ランダム』に選ぶのが原則ということです。
先程のプロ野球の例であれば、日本国民全員の名前をくじ引きの箱の中に入れ、その中から1つずつ引いて選ばれた回答者1000人にアンケートに答えてもらうとか・・・です。
“自分の知り合いの知り合いとかを辿って1000人集めよう！”なんて方法もありますが、これだとランダムとは言えません。
自分自身がプロ野球ファンだとしたら、知り合いにもプロ野球ファンが多いことが想定されますからね。そのため回答者を募集する環境がランダムではなくプロ野球ファンが多い環境の中で募集していることになるので、実状よりもプロ野球ファンが多いというアンケート結果が出てきてしまう恐れがあるのです。
このようにランダムな状況で回答者を選ぶことを『ランダムサンプリング（無作為抽出）』と言います。正しいアンケート調査を行うのであれば、この原則に則って回答者を選ばなければいけません。
しかし実際には、完璧なランダムサンプリングを行うことはかなり難しいです。先ほどのようなくじ引き装置はない訳ですからね。
従いまして完璧ではないにしても、できるだけランダムに近い環境でアンケートを行うことが大事になってきます。その為によく行われているのが『アンケートモニターパネル』を利用した調査です。知り合いなどの伝手を辿るよりもかなり正確なアンケートが行えます。多少お金はかかりますが、こういったものを積極的に活用して正確なアンケートを行って欲しいのです。
※アンケートモニターパネルの詳細はこちらのブログでも紹介しています！
どのくらいの誤差が発生するのか？
サンプルと母集団の間の誤差
例えばあるカバンメーカーのランドセルを購入した人が合計1万人いたとして、この方々に対してランドセルの商品満足度を調査するとします。
ということはこの調査の母集団の規模は『1万人』であり、この人たち全員から回答をもらえるのであれば一番正確な結果がアウトプットできます。その結果が1万人全員の”総意”ですから、これ以上正確な調査はありません。
但し全員に聴くことは相当大変な作業になるので、その中の一部の人に回答を依頼する訳です。
そして1,000人が回答してくれたのであれば、その1,000人の回答結果を使って母集団（1万人）の状況を推定することになります。これがアンケート調査の本質でしたよね。
ただ何度も言う通り、このアンケートで算出されるのは母集団の『推定値』であるということです。
要するに1,000人のアンケート結果で内容量を大変重視している人が40%だったとしても、母集団（1万人）で調査をしたらぴったり40%になるかどうかは分かりません。おそらく多少ズレた数値になると思うのですが、この”サンプル調査の数値”と”母集団を全数調査した時の数値”のズレを『誤差（標本誤差）』と呼ぶ訳です。
サンプル誤差の早見表
しかしこれは少し分かりにくいのですが、具体的に何％の誤差が発生していると断定することはできません。
母集団全体での全数調査はやっていないですから、全数調査とサンプル調査の差が具体的にいくつか？なんて分からないのです。
ただ『このくらいの誤差が発生している可能性がある』と計算することはできます。・・・ややこしいですよね。
取り急ぎ、その誤差表を以下に書きました。どのように計算すればこれが出てくるのかは後で説明しますが、例えば先ほどのランドセルの調査では。購入した人1000人の中に『内容量』を大変重視している人が40%いたという結果でした。
その場合、サンプルサイズ：1000人で比率40%のところを見てほしいのですが、誤差は『±3.0%』とあります。
従いまして、今回のアンケート(サンプル調査)では40%でしたが、母集団全体で全数調査を行えば、内容量の重視度は40 ± 3.0%=37%～43%の間にあるはずだと考えられる訳です。
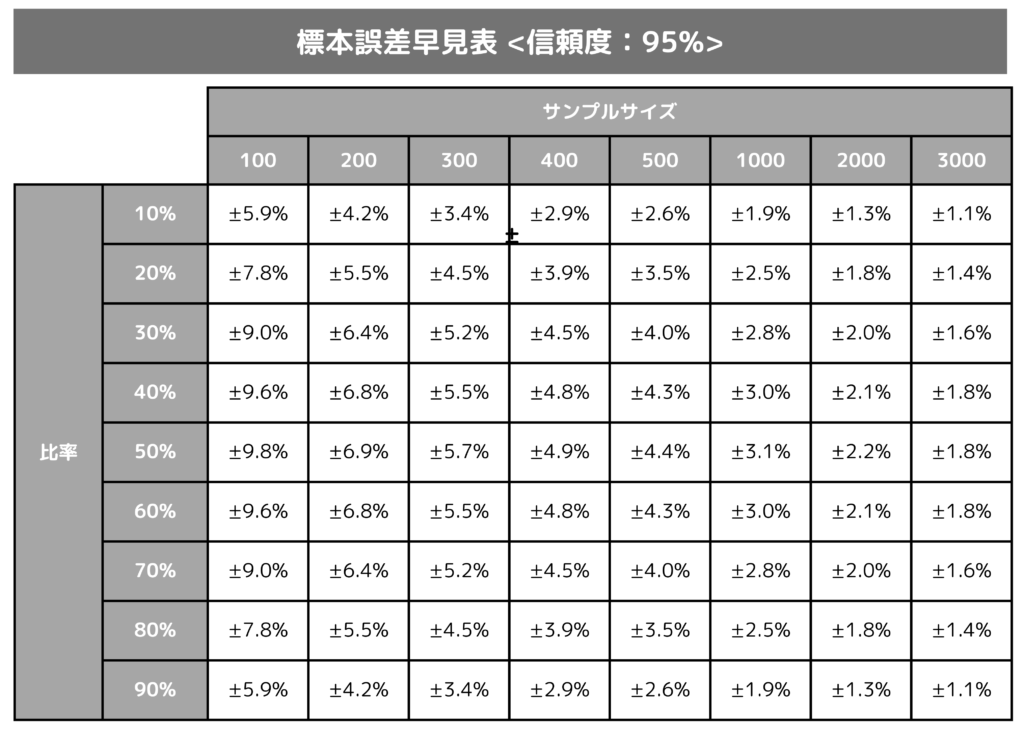
この表をよく眺めて欲しいのですが、サンプルサイズが多くなればなるほど誤差も小さくなっていくのが分かりますよね。
また更に縦の比率を見ると、誤差が一番大きいのは比率：50%の時であることも見て取れます。
しかし当然のことながら、この比率というのは調査をする前には分かりません。
先ほどのランドセルの例もそうですが、それぞれの項目を重視する人が何%いるのか？という比率がが分からないからこそアンケート調査をしている訳ですからね。
ただ裏を返せば、調査を実施する前に『最大でどのくらいの誤差が発生しそうなのか』は先ほどの表の比率：50%の部分の誤差を参考にすればよいです。
結果的に比率が何%になろうが、この50%の時の誤差以上にはならないはずです。
信頼度って何？
ちなみに新しい統計学の用語が出てきて拒否反応を示す方も多いと思いますが、もう少し補足をすると”40±3.0%”という風に幅を持たせて母集団での比率を推定することを『区間推定』と言います。
そして先ほどの誤差表は『信頼度：95%』で計算した時のモノです。これは調査と区間推定を100回実施したら、95回はこの区間に母集団の比率が入るということを表しています。
この信頼度：95%というのは結構高い値です。
同じアンケート調査を100回やったら95回はこの範囲内に収まる訳ですから、ほぼこの範囲から外れることは確率的にかなり少ないと言えます。
ただもっと厳密な調査をするのであれば信頼度を99%くらいまで上げて区間推定しても良いですし、もう少しゆるくして90%程度にすることも可能です。その辺は実際に集計・分析を担当する人が決めてしまって構わないのですが、通常のマーケティングリサーチでは信頼度：95%で誤差を計算し分析することが多いと考えて下さい。
【補足】標本誤差の計算式
上記の早見表を是非参考にしてほしいのですが、もう少し統計学的にこの話を理解したい人の為に計算式を紹介します。
(統計学があまり得意でない方は読み飛ばして下さい。)
先程も書いた通り、“標本誤差”というのは母集団からサンプルを抽出して調査を行った際、そのサンプル比率と母集団での比率の差を言います。
そして仮に何度も調査を行うとこの標本誤差自体にもバラツキが生じる訳ですが、そのバラツキは正規分布に従います。
そしてその分布の標準誤差(サンプル比率の標準偏差)は以下の式で計算できます。
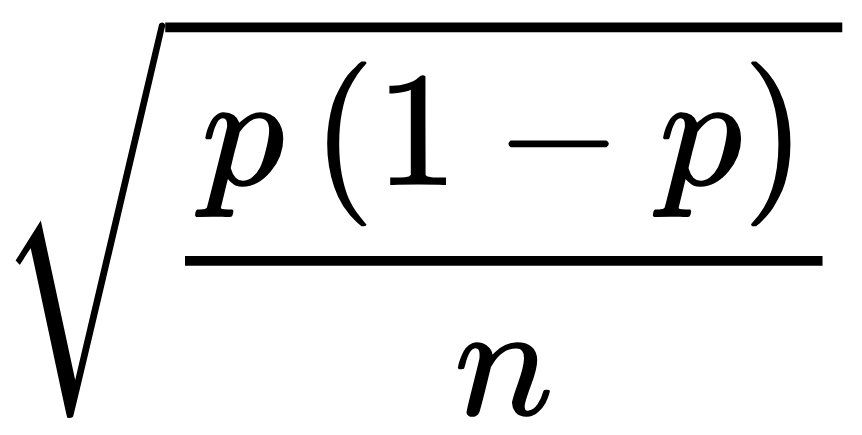
ちなみにpは母比率(母集団での比率)、nはサンプルサイズです。ということは、95%信頼区間における誤差：eはこれに1.96をかけた
ということになります。
先程の早見表は上記の式によって計算していて『95%の確率で母比率はこの範囲内にある』ということになります。
ややこしいのはpは未知である“母比率”であるということです。
ということはこの式でeを求めることができないのですが、結論としてはこのpにはサンプル比率を入れて構いません。
なぜならば上記の場合は母比率を中心とした時に95%信頼区間でサンプル比率はどの程度バラつくのかを求めているのに対し、pにサンプル比率を入れることで、“サンプル比率を中心とした時に95%信頼区間で母比率を値はどの範囲にあるかを推定していることになるからです。
標本誤差計算フームはこちら！
標本誤差をもう少し細かく計算したい人の為にフォームを準備しました。
以下のツールにサンプル比率とサンプルサイズ、信頼度を入力すると誤差が計算できます。
是非活用してみて下さい。
